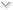Why there is always a J window open on my desktop

People often ask me what tools I use for data analysis. My usual answer is SQL and I explain that just as Willie Sutton robbed banks because "that's where the money is," I use SQL because that is where the data is. But sometimes, it gets so frustrating trying to figure out how to get SQL to do something as seemingly straight forward as a running total or running maximum, that I let the data escape from the confines of its relational tables and into J where it can be free. I assume that most readers have never heard of J, so I'll give you a little taste of it here.  It's a bit like R only a lot more general and more powerful. It's even more like APL, of which it is a direct descendant, but those of us who remember APL are getting pretty old these days.

The question that sent me to J this time came from a client who had just started collection sales data from a web site and wanted to know how long they would have to wait before being able to make some statistically valid conclusions about whether spending differences between two groups who had received different marketing treatments were statistically significant. One thing I wanted to look at was how much various measures such as average order size and total revenue fluctuate from day to day and how many days does it take before the overall measures settle down near their long-term means. For example, I'd like to calculate the average order size with just one day's worth of purchases, then two day's worth, then three day's worth, and so on. This sort of operation, where a function is applied to successively longer and longer prefixes is called a scan.

A warning: J looks really weird when you first see it. One reason is that many things that are treated as a single token are spelled with two characters. I remember when I first saw Dutch, there were all these impossible looking words with "ij" in them--ijs and rijs, for example. Well, it turns out that in Dutch "ij" is treated like a single letter that makes a sound a bit like the English "eye." So ijs is ice and rijs is rice and the Rijn is a famous big river. In J, the second character of these two-character symbols is usually a '.' or a ':'.

=: is assignment. <. is lesser of. >. is greater of. And so on. You should also know that anything following NB. on a line is comment text.

   x=: ? 100#10                        NB. One hundred random integers between 0 and 9

   +/ x                                      NB. Like putting a + between every pair of x--the sum of x.
424
   <. / x                                    NB. Smallest x
0
   >. / x                                    NB. Largest x
9
   mean x
4.24
   ~. x                                      NB. Nub of x. (Distinct elements.)
3 0 1 4 6 2 8 7 5 9
   # ~. x                                    NB. Number of distinct elements.
10
    x # /. x                                  NB. How many of each distinct element. ( /. is like SQL GROUP BY.)
6 10 15 13 15 9 9 12 6 5
   +/ \ x                                      NB. Running total of x.
3 3 4 8 12 13 19 23 25 33 41 48 54 56 61 67 69 72 73 74 75 . . .
   >./ \ x                                     NB. Running maximum of x.
3 3 3 4 4 4 6 6 6 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 9 9 9 9 9 . . .
   mean \ x                                  NB. Running mean of x.
3 1.5 1.33333 2 2.4 2.16667 2.71429 2.875 2.77778 3.3 3.72727 . . .
   plot mean \ x                            NB. Plot running mean of x.

   plot var \ x                               NB. Plot running variance of x.

 

 

J is available for free from J software. Other than as a fan, I have no relationship with that organization.