Loading IP Test Data Into Postgres

Recently, I was trolling around the internet looking for some IP address data to play with.  Fortunately, I stumbled across MaxMind's Geolite Database, which is available for free.    All I have to do is include this notice:

This product includes GeoLite2 data created by MaxMind, available from <a href="http://www.maxmind.com">http://www.maxmind.com</a>.

That's easy enough.  The next question is how to get this into my local Postgres database.  A bit over a year ago, I very happily gave up on my Dell computer and opted for a Mac.  One downside to a Mac is that SQL Server doesn't run on it (obviously my personal opinion).  Happily, Postgres does and it is extremely easy to install by going to postgresapp.com.   An interface similar enough to SQL Server Management Studio (called pgadmin3) is almost as easy to install by going here.

So, the next problem is getting the MaxMind data into Postgres.  Getting the two tables into Postgres is easy, using the copy command.  The challenge is IPV6 versus IPV4 addresses.  The data is in IPV6 format with a subnet mask to represent ranges.  Most of us who are familiar with IP addresses are familiar with IPV4 addresses.  These are 32 bits and look something like this:  173.194.121.17 (this happens to be an address for www.google.com attained by running ping www.google.com in a terminal window).  Alas, the data from MaxMind uses IPV6 values rather than IPV4.

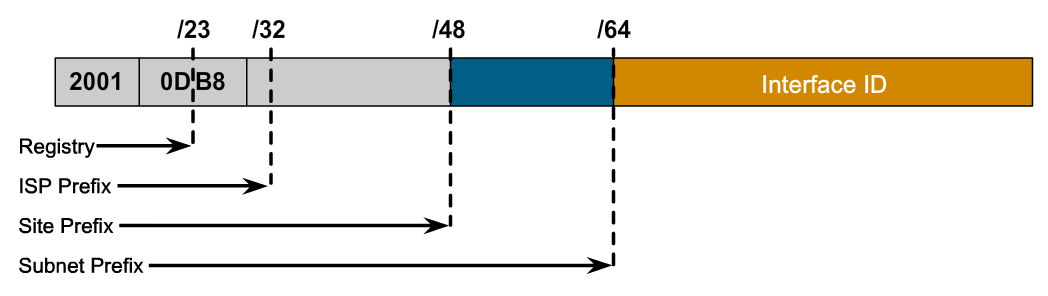
In IPV6, the above would look like: ::ffff:173.194.121.17 (to be honest, this is a hybrid format for representing IPV4 addresses in IPV6 address space).  And the situation is a bit worse, because these records contain address ranges.  So the address range is really:  ::ffff:173.194.0.0/112.

The "112" is called a subnet mask.  And, IPV4 also uses them.  In IPV4, they represent the initial range of digits, so they range from 1-32, with a number like "24" being very common.  "112" doesn't make sense in a 32-bit addressing scheme.   To fast forward, the "112" subnet mask for IPV6 corresponds to 16 in the IPV4 world.  This means that the first 16 bits are for the main network and the last 16 bits are for the subnet.  That is, the addresses range from 173.194.0.0 to 173.194.255.255.  The relationship between the subnet mask for IPV6 and IPV4 is easy to express:  the IPV4 subnet mask is the IPV6 subnet mask minus 96.

I have to credit this blog for helping me understand this, even though it doesn't give the exact formula.  Here, I am going to shamelessly reproduce a figure from that blog (along with its original attribution):

Courtesy of ls-a.org

This figure says  the following.  The last 64 bits are new to IPV6, so they can be automatically subtracted out of the subnet mask.  Then, bits 0-32 also seem to be new, so they can also be subtracted out.  That totals 96 bits in the new version not in the old version.  To be honest, I am not 100% positive about my interpretation.  But it does seem to work.  Google does indeed own exactly this address range.

The Postgres code for creating the table then goes as follows:

create table ipcity_staging (
    network_start_ip varchar(255),
    network_mask_length int,
    geoname_id int,
    registered_country_geoname_id int,
    represented_country_geoname_id int,
    postal_code varchar(255),
    latitude decimal(15, 10),
    longitude decimal(15, 10),
    is_anonymous_proxy int,
    is_satellite_provider int
);

copy public.ipcity_staging
    from '...data/MaxMind IP/GeoLite2-City-CSV_20140401/GeoLite2-City-Blocks.csv'
    with CSV HEADER;

create table ipcity (
    IPCityId serial not null,
    IPStart int not null,
    IPEnd int not null,
    IPStartStr varchar(255) not null,
    IPEndStr varchar(255) not null,
    GeoNameId int,
    GeoNameId_RegisteredCountry int,
    GeoNameId_RepresentedCountry int,
    PostalCode varchar(255),
    Latitude decimal(15, 10),
    Longitude decimal(15, 10),
    IsAnonymousProxy int,
    IsSatelliteProvider int,
    unique (IPStart, IPEnd),
    unique (IPStartStr, IPEndStr)
);

insert into ipcity(IPStart, IPEnd, IPStartStr, IPEndStr, GeoNameId, GeoNameId_RegisteredCountry, GeoNameId_RepresentedCountry,
                   PostalCode, Latitude, Longitude, IsAnonymousProxy, IsSatelliteProvider
                  ) 
    select IPStart, IPEnd, IPStartStr, IPEndStr, GeoName_Id, registered_country_geoname_id, represented_country_geoname_id,
           Postal_Code, Latitude, Longitude, Is_Anonymous_Proxy, Is_Satellite_Provider
    from (select network_mask_length - 96,
                 hostmask(inet (substr(network_start_ip, 8) || '/' || network_mask_length - 96)) ,
                 inet(host(inet (substr(network_start_ip, 8) || '/' || network_mask_length - 96) )) |
                 hostmask(inet (substr(network_start_ip, 8) || '/' || network_mask_length - 96)
                ) as ipend_inet,
                substr(network_start_ip, 8) || '/' || network_mask_length - 96,
                ((split_part(IPStartStr, '.', 1)::int << 24) +
                 (split_part(IPStartStr, '.', 2)::int << 16) +
                 (split_part(IPStartStr, '.', 3)::int << 8) +
                 (split_part(IPStartStr, '.', 4)::int)
                ) as IPStart,
                ((split_part(IPEndStr, '.', 1)::int << 24) +
                 (split_part(IPEndStr, '.', 2)::int << 16) +
                 (split_part(IPEndStr, '.', 3)::int << 8) +
                 (split_part(IPEndStr, '.', 4)::int)
                ) as IPEnd,
                st.*
          from (select st.*,
                       host(inet (substr(network_start_ip, 8) || '/' || network_mask_length - 96)) as IPStartStr,
                       host(inet(host(inet (substr(network_start_ip, 8) || '/' || network_mask_length - 96) )) |
                            hostmask(inet (substr(network_start_ip, 8) || '/' || network_mask_length - 96))
                           ) as IPEndStr
                from ipcity_staging st 
                where network_start_ip like '::ffff:%'
               ) st
         ) st;

Armed Bandits: A Statistical Approach

This is a continuation of my previous post on multi-armed bandits.  And, I'm guessing there will be at least one more after this.

The Multi-Armed Bandit problem is a seemingly simple problem.  A gambler is faced with a row of slot machines, each of which returns a different winning.  S/he need to devise a strategy to find the winningest slot machine as quickly as possible and then just play that one.

Most of the strategies for doing this are based on a greedy-algorithm approach.  They are some variation on:  randomly (or round robinly) choose slot machines until some threshold has been reached.  Then continue playing the winningest one.  These actually work pretty well.  But I am interested in applying basic statistics to this.

Before doing that, let me explain why I am interested.  Imagine that I have a web site and I have an ad space to fill.  Here are different things I might put there:

• A run of network ad that will make some amount of money per impression.
• A click-through ad that will make some amount of money if someone clicks on it.
• A partner ad that will make some amount of money if someone signs up for something.

The Multi-Armed Bandit provides an automated means of testing all three of these at once, along with variations that may, or may not, prove better than business-as-usual.   I think of it as automated champion-challenger models.

Here is a "statistical" approach to this problem.  Let me assume that there are N campaigns being run.   Each campaign has a payout distribution.  I can calculate the average payout for each campaign.  In the end, I want to choose the campaign that has the largest average payout.  Note that I'm make assumptions here that the the campaigns perform consistently across time and across the visitor population.  Those are other issues I discussed earlier.  Let's focus on the basic problem here.

By the Central Limit Theorem, we know that we can estimate the average based on a sample of data.  This estimate of the average has an average and a standard deviation, which (once there are enough samples) gets smaller and smaller, meaning that the average is better and better.

The idea is then simple.  At the beginning, give each campaign the same estimate with a wide confidence interval.  The intervals all overlap completely, so the choice of best campaign is random.  Initially, we might want to round-robin the data to get some initial values.  Relatively quickly, though, we should get estimates for each of the campaigns; these will be inaccurate but they will have wide confidence intervals.

At each iteration, we need to update the average and standard deviation.  Fortunately, there are easy incremental algorithms for both, so all the historical data does not need to be saved.  This article discusses various algorithms for calculating variance, and hence standard deviation.

The question is:  if we have multiple averages and standard errors, how do we choose the appropriate campaign at each step.  We can run a fast simulation to get the best campaign.  For each campaign, generate a random number based on the estimated average and standard error.  Choose the campaign that has the largest number.

What happens over time is that the campaign with the best payout should become more and more confident, as well as having the highest average.   Its confidence interval will shift way from the others, further increasing the odds of that campaign being chosen.  This is a positive feedback mechanism.  Note that I am using the term "confidence interval" as an aid to visualizing what is happening; this method is not actually using any p-values generated from the confidence interval.

One nice feature about this method is that it can adapt to the chosen solution getting worse.  If so, the average will decrease (but not the standard error) and other campaigns might be chosen.  Getting this to work involves a bit more effort, because you probably want to keep the sample size fixed -- otherwise the learning rate would be too small.

A note about distributions.  This solution is depending onto the distribution of the sample average, not the distribution of the original payout.  The sample average should (in the limit) have a  normal distribution, characterized by the average and standard error.  This is not a statement about the original data distribution, only about the average.  And, in the end, we want to choose the campaign that has the best average.  This is handy, because the three examples that I gave earlier are very different.  One has a constant (but low) payout and the other two are biased toward zero payouts.

I do believe that this method will produce reasonable results in practice.  However, it does bring up subtle issues about how the underlying distributions of the payouts affect the averages.  On the surface, it seems pretty sound, and it should work pretty well in practice.

Measuring Site Engagement: Pages or Sessions

One of our clients is a large media website that faced a simple question: What is the best way to find the most engaged users on the web site? The goal was to focus a marketing effort on these users.

A media web site is challenging, because there is no simple definition of engagement or customer worth. The idea is that engagement can either lead to more advertising views or to longer subscriptions, depending on the business model for the site. On the other hand, for a retailing site, the question is simpler, because there is a simple method to see who the best customers are. Namely, the amount of money they spend.

Engagement is a nice marketing concept, but how can it be defined in the real world? One way is to simply look at the number of page views during some period of time. Another is to look at the number of sessions (or alternatively days of activity if sessions are not available) during a specified period of time. Yet another is to measure breadth of usage of the site over a period of time: Does the user only go to one page? Is the user only coming in on referrals from Google?

The first analysis used one month of data to define engagement. The top users for one month were determined based on pages and sessions. Of course, there is a lot of overlap between the two groups -- about 60% of the top deciles overlapped.

Which group seems better for defining engagement, the top users by page views or by sessions? To answer this, let's borrow an idea from survival and measure how many users are still around nine months later. (Nine months is arbitrary in this case). In this case, the return rate for the top decile for sessions was 74.4% but for the top decile for pages was lower at 73.8%. Not a big difference, but one that suggests that sessions are better.

Actually, the results are even more striking for visitors who are not in both top deciles. For the non-overlapping group, the session return rate is69.6% versus 67.9% for the page deciles.

For defining engagement, we then extended these results to three months instead of one to find the top one million most engaged users. The three measures are:

1. Visitors that have the most page views over three months.
2. Visitors that have the most sessions over three months.
3. Visitors in the top tercile of sessions (third) in each month, then take the highest terciles.

Three months was chosen as a rather arbitrary length of time, because the data was available. Holding it constant also lets us understand the difference between sessions and page views.

These three methods all produced about the same number of visitors -- the goal was to find the top one million most engaged users.

By these measures, the top one million visitors chosen by the three methods had the following "return" rates, nine months later:

1. Page views in three months: 65.4%
2. Sessions in three months: 65.9%
3. Sessions over three months: 66.9%

The nine-month survival suggests that the sessions over three months is the better approach for measuring engagement.

Counting Users From Unique Cookies

Counting people/unique visitors/users at web sites is a challenge, and is something that I've been working on for the past couple of months for the web site of a large media company. The goal is to count the number of distinct users over the course of a month. Counting distinct cookies is easy; the challenge is turning these into human beings. These challenges include:

• Cookie deletions. A user may manually delete their cookies one or more times during the month.


• Disallowing first party cookies. A user may allow session cookies (while the browser is running), but not allow the cookies to be committed to disk.


• Multiple browsers. A single user may use multiple browsers on the same machine during the month. This is particularly true when the user upgrades his or her browser.


• Multiple machines. A single user may use multiple machines during the month.

And, I have to admit, that the data that I'm using has one more problem, which is probably not widespread. The cookies are actually hashed into four bytes. This means that it is theoretically possible for two "real" cookies to have the same hash value. Not only theoretically possible, but it happens (although not too frequently).

I came across a very good blog by Angie Brown that lays out the assumptions in making the calculation, including a spreadsheet for varying the assumptions. One particularly interesting factoid from the blog is that the number cookies that appear only once during the month exceeds the number of unique visitors, even under quite reasonable assumptions. Where I am working, one camp believes that the number of unique visitors is approximated by the number of unique cookies.

A white paper by ComCast states that the average user has 2.5 unique cookies per month due to cookie deletion. The paper is here, and a PR note about it is it is here. This paper is widely cited, although it has some serious methodological problems due to the fact that its data sources are limited to DoubleClick and Yahoo!.

In particular, Yahoo! is quite clear about its cookie expiration policies (two weeks for users clicking the "keep me logged in for 2 weeks" box and eight hours for Yahoo! mail). I do not believe that this policy has changed significantly in the last few years, although I am not 100% sure.

The white paper from ComCast does not mention these facts, which means that most of the cookies that a user has are due to automatic deletion, not user behavior. How many distinct cookies does a user have, due only to the user's behavior?

If I make the following assumptions:

• The Yahoo! users have an average of 2.5 cookies per month.


• ComCast used the main Yahoo! cookies, and not the Yahoo! mail cookies.


• All Yahoo! users use the site consistently throughout the month.


• All Yahoo! users have the "keep me logged in for 2 weeks" box checked.

Then I can estimate the number of cookies per user per machine per month. The average user would have 31/14 = 2.2 cookies per month, strictly due to the automatic deletion. This leaves 0.3 cookies per month due to manual deletion. Of course, the user starts with one cookie. So the average number of cookies per month per user per machine is 1.3.

By the way, I find this number much more reasonable. I also think that it misses the larger source of overcounting -- users who use more than one machine. Unfortunately, there is no single approach. In the case that I'm working on, we have the advantage that a minority of users are registered, so we can use them as a sample.