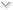Multidimensional Chi-Square, Expected Values, Independence, and All That, Part 1

When I speak about data mining, I often refer to the chi-square test as my favorite statistical test. I should be more specific, though, because I am really refering to the two-dimensional chi-square test. This is described in detail in Chapter 3 of Data Analysis Using SQL and Excel, a book that I do heartily recommend and is the starting point for many ideas that I write about here.

The chi-square test can be applied to more than two dimensions. However, the multi-dimensional chi-square behaves a bit differently from the two-dimensional case. This posting describes why. The next posting describes the calculation for the multi-dimensional chi-square. And the third posting in this series will describe how to do the calculations using SQL.

Fast Overview of Chi-Square

The Chi-Square test is used when we have two or more categorical variables and counts of how often each combination appears. For instance, the following is a simple set of data in two dimensions:

	A=0	B=0	1
	A=0	B=1	2
	A=1	B=0	3
	A=1	B=1	4

This data is summarized from ten observations. The first row says that in one data record, both A and B are zero. The last row says that in four of them, both A and B are 1. In practice, when using the chi-square test, we would want higher counts -- and we would get them, because these are counts of customers (say, responders and non-responders by gender).

In two dimensions, a contingency table is perhaps a better way of looking at the counts:

		B=0	B=1
	A=0	1	2
	A=1	3	4

The chi-square test then asks the question . . . What is the probability that the counts are produced randomly, assuming that both the A and B are independent? To answer this question, we need the expected values assuming independence between A and B. The following table shows the expected values:

		B=0	B=1
	A=0	1.2	1.8
	A=1	2.8	4.2

The expected values have two important properties. First, the row sums and column sums are the same as the original data. So, 1+2 = 1.2+1.8 = 3, and so on for both rows and both columns.

The second property is a little more subtle, but it says that the ratios of values in any column or any row are the same. So, 1.2/1.8 = 2.8/4.2 = 2/3, and so on. Of all possible 2X2 matrices, there is only one that has both these properties.

Now, the chi-square value for any cell is the square of the difference between the actual value and the expected value divided by the expected value. The chi-square for the matrix is the sum of the chi-square values for all the cells. These follow a chi-square distribution with one degree of freedom, and this gives us a enough information to determine whether the original counts are likely due to chance.

Calculating expected values is easy. The expected value for any cell is the product of the row sum times the column sum divided by the total in the table. For example, for A=0, B=0, the row sum is 3 and the column sum is 4. The product is 12, so the expected value is 1.2 = 12/10.

Treating Three Dimensions As Two Dimensions
Now, let's assume that the data has three dimensions rather than two. For example:

	A=0	B=0	C=0	1
	A=0	B=0	C=1	2
	A=0	B=1	C=0	3
	A=0	B=1	C=1	4
	A=1	B=0	C=0	5
	A=1	B=0	C=1	6
	A=1	B=1	C=0	7
	A=1	B=1	C=1	8

We can treat this as a contingency table in two dimensions:

		C=0	C=1
	A=0,B=0	1	5
	A=0,B=1	2	6
	A=1,B=0	3	7
	A=1,B=1	4	8

And from this we can readily calculate the expected values:

		C=0	C=1
	A=0,B=0	1.67	4.33
	A=0,B=1	2.22	5.78
	A=1,B=0	2.78	7.22
	A=1,B=1	3.33	8.67

The chi-square calculation follows as in the earlier case. The chi-square value for each cell is the actual count minus the expected value squared divided by the expected value. The chi-square value for the entire table is the sum of all the chi-square values for each cell.

The only difference here is that there are three degrees of freedom. This affects how to transform the chi-square value into a probability, but it does not affect the computation.

Which Are the Right Expected Values?
There are actually two other continency tables that we might produce from the original 2X2X2 data, depending on which dimension we use for the columns:

		B=0	B=1
	A=0,C=0	1	2
	A=0,C=1	5	6
	A=1,C=0	3	4
	A=1,C=1	7	8

and

		A=0	A=1
	B=0,C=0	1	3
	B=0,C=1	5	7
	B=1,C=0	2	4
	B=1,C=1	6	8

Following the same procedure, we can calcualte the expected values for each of these.

		B=0	B=1
	A=0,C=0	1.33	1.67
	A=0,C=1	4.89	6.11
	A=1,C=0	3.11	3.89
	A=1,C=1	6.67	8.33

and

		B=0	B=1
	A=0,C=0	1.78	2.22
	A=0,C=1	5.33	6.67
	A=1,C=0	2.67	3.33
	A=1,C=1	6.22	7.78

Oops!. The three sets of expected values are different from each other. Which do we use for the 2X2X2 chi-square calculation?

Why Independence is a Strong Condition
The answer is none of these. For the three dimensional data (and higher dimensional as well), the three contingency tables are almost always going to be different, because they mean different things. This is perhaps best viewed geometrically:


In this cube, the front face corresponds to C=0 and the hidden face to C=1. The A values go horizontally and the B's vertically. The three different contingency tables are formed by cutting the cube in half and then pasting the halves together. These tables are different.

For instance, the front face and the back facee are each 2X2 contingency tables. The expected values for these can be determined just from the information on each face. We do not need the information along the C dimension for this calculation. Worse, we cannot even use this information -- so there is no way to ensure that the sums along the "C" dimension add up to the same values in the original data and for the expected values.

The problem is that the sums along each dimension overspecify the problem. A given value has three adjacent values along three dimensions. However, only two of the dimensions are needed to calcualte an expected value, assuming independence along those two dimensions. The information along the third dimension cannot be incorporated into the calculation.

The reason? Independence is a very strong condition. Remember, it says not only that the sums are the same but also that the ratios within each row (or column or layer) are the same. Normally, we might think "independent" variables are providing as much flexibility as possible. However, that is not the case. In fact, the original counts are the only ones that meet the all the conditions of independence at the level of every row, colum, and level.

When I think of this situation, I think of a paradox related to the random distribution of stars. We actually perceive a random distribution as more ordered. Check out this site for an example. Similarly, our intuition is that independence among variables is a weak condition. In fact, it can be quite a strong condition.

The next posting will explain how expected values work in three and more dimensions. For now, it is worth explaining that converting a three-dimensional problem into two dimensions is often feasible and reasonable. This is particularly true when one of the dimensions is a "response" characteristic and the rest are input dimensions. However, such a 2X2 table is really an approximation.

MapReduce and SQL Aggregations Using Grouping Sets

In an earlier post, I compared MapReduce functionality and and SQL functionality and made the claim that SQL required two passes through the data to calculate the number of customer starts and stops per month. (The data used for this is on the companion web site for my book .)

Two of the comments on this post explained SQL syntax that achieves the goal more efficiently. In particular, the GROUPING SETS keyword, which is part of more recent SQL standards, is an efficient solution that allows SQL to do more of the types of processing made possibly by MapReduce. This functionality is available in SQL Server and Oracle. However, it is not yet available in MySQL.

The following SQL query answers the question at the top of this post using FULL OUTER JOIN (an alternative approach is to use UNION ALL):

SELECT m, ISNULL(numstarts, 0), ISNULL(numstops, 0)
FROM (SELECT MONTH(start_date) as m, COUNT(*) as numstarts
......FROM customer c
......GROUP BY MONTH(start_date)
.....) start FULL OUTER JOIN
.....(SELECT MONTH(stop_date) as m, COUNT(*) as numstops
......FROM customer c
......GROUP BY MONTH(stop_date)
.....) stop
.....ON start.m = stop.m

Although this query is effective, in most databases, it would require two passes through the data.

An alternative approach is to use GROUPING SETS. This keyword is a generalization and imporvement on CUBE functionality. The generalization is more powerful, because it gives more options for the query optimizaer.

GROUPING SET allows a query to return summaries along each grouping dimension, with or without generating the full set of rows that GROUP BY would create. The following query returns a separate row for each combination of start month and stop month:

SELECT MONTH(start_date) as start_month, MONTH(stop_date) as stop_month,
.......COUNT(*) as cnt
FROM customer
GROUP BY MONTH(start_date), MONTH(stop_date)

We could imagine row in the result set as being a cell in a big cross tabulation table, with the start months on the rows and the stop months on the columns. What we really want are the subtotals along the rows and the columns, not the full table. The following query accomplishes this:

SELECT COALESCE(start_month, stop_month) as month,
.......SUM(CASE WHEN stop_month IS NULL THEN cnt ELSE 0 END) as starts,
.......SUM(CASE WHEN start_month IS NULL THEN cnt ELSE 0 END) as stops
FROM (SELECT MONTH(start_date) as start_month, MONTH(stop_date) as stop_month,
.............COUNT(*) as cnt
......FROM customer
......GROUP BY GROUPING SETS (MONTH(start_date), MONTH(stop_date))
.....) a
WHERE start_month IS NOT NULL and stop_month IS NOT NULL

The subquery in this query aggregates the data in a special way. The outer query simply reformats the results to be similar to the earlier query.

The GROUPING SETS keyword specifies that summaries of the data should be returned, rather than the individual aggregated rows. This syntax specifies that groups are created for the start month and stop month. So, the inner query returns rows such as the following:

	Start Month	Stop Month	Count
	Jan	NULL
	Feb	NULL
	. . .
	NULL	Jan
	NULL	Feb
	. . .

However, the cross-rows generated by the regular group by are not there. Half the rows have the subtotals for start months; for these the stop month column is NULL. Half have subtotals for the start month, where the stop month is NULL. This syntax does not generate the cross-tabulation data, but it does keep the row and column subtotals.

The GROUPING SETS keyword generates the subtotals for the start months and stop months. In general, the query optimizer will generate the various grouping aggregations in one pass over the data. This makes the syntax and performance much more similar to the MapReduce approach.

However, Map Reduce still has two practical advantages. The first are the limits on the number of groups in the grouping sets. In SQL Server, only 32 groups are allowed. This example only used two. But more complex examples might breach this limit.

The other issue is the flexibility of the SQL language. One of the major uses of MapReduce is to process text. In this case, we would be extracting many potential features from the text, and then doing subsequent aggregations. SQL extensions can be used to create the features. However, such features quickly exceed the limits on the number of groups, limiting the feasbility of this approach.

One warning about the syntax. The parentheses in the GROUPING SETS statement are important. The following version would actually be the equivalant of the regular GROUP BY:

GROUP BY GROUPING SETS ((MONTH(start_date), MONTH(stop_date))

This is because the keyword takes a list of things being grouped. So, in the original version (one set of parentheses), there are two elements in the list -- the totals for start month and stop month. In the second version, there is one element in the list, so the cross-tabulation between start month and stop month are generated instead. This cross-product is the equivalent of the regular group by.

And my final comment is about the CUBE keyword which seems to provide the same functionality. This keyword generates all the regular aggregation rows in the table, along with additional subtotals for all combinations of dimensions. In the above example, it would generate the cross-tab table of start month and end month, as well as the summary rows.

The problem with the CUBE keyword is that the original query does not need all the aggregation rows, so generating them is a waste of time. Whether this is faster or slower than the original version of the query with the FULL OUTER JOIN depends on the environment. However, it could be quite inefficient. In addition, the query optimizer would have a very difficult time determining that these rows are not needed.

I do not feel that the CUBE keyword provides functionality similar to MapReduce. However, the GROUPING SETS keyword does provide functionality similar to MapReduce, because it produces summaries along dimensions without requiring multiple passes through the data and without generates large cross-tabulations. In addition, the GROUPING SETS keyword allows the query optimizer to choose from a variety of algorithms for executing the query, taking advantage of large computer systems using SQL syntax instead of programming.

Accounting for Variation in Variables Between- and Within- Groups

Recently, I had occasion to learn about fixed effects and random effects models (as well as the larger subject known as hierchical or multi-level modeling) in the context of analyzing patient longitudinal data. This posting is about one particular question that interested me in this work: For a given variable, how much of the variation in the values is due to within-group effects versus how much is due to between-group effects.

For the longitudinal patient data, the groups were repeated measurements on the same individual. For this discussion though, I'll ask questions such as "How much of the variation in zip code population is due to variations within a state versus variations between states?" I leave it to the reader to generalize this to other areas.

The data used is the census data on the companion web site to my book . Also, the spirit of understanding this problem using SQL and charts also comes from the book.

This posting starts with what I consider to be a simple approach to answering the question. It is then going to show how to calculate the result in SQL. Finally, I'm going to discuss the solution Paul Allison prsents in his book, and what I think are its drawbacks.

What Does Within- Versus Between- Group Variation Even Mean?

I first saw this issue in Paul Allison's book Fixed Effects Regression Methods for Longitudinal Data Analysis Using SAS, which became something of a bible on the subject while I was trying to do exactly what the title suggested (and I highly, highly recommend the book for people tackling such problems). On page 40, he has the tantalizing observation "The degree to which the coefficients change under fixed effects estimation as compared with conventional OLS appears to be related to the degree of between- versus within-school variation on the predictor variables."

This suggests that within-group versus between-group variation can be quite interesting. And not just for predictor variables. And not just for schools.

Let's return to the question of how much variation in a zip code's population is due to the state where the zip code resides, and how much is due to variation within the state. To answer this question analytically, we need to phrase it in terms of measures. Or, for this question, how well does the average population of zip codes in a state do at predicting the population of a zip code in the state?

In answering this question, we are replacing the values of individual zip codes with the averaged values at the group (i.e. state) level. By eliminating within group variation, the answer will tell us about between-group variation. We can assume that remaining variation is due to within group variation.

Using Variation to Answer the Question
Variance quantifies the idea that each point -- say the population of each zip code -- differs from the overall average. The following chart shows a scatter plot of all the zip codes with the overall average (by the way, the zip codes here are ordered by the average zip code population in each state).

The grey line is the overall average. We can see that the populations for zip codes are all over the place; there is not much of a pattern. As for the variance calculation, imagine a bar from each point to the horizontal line. The variance is just the sum of the squared distances from each point to the average. This sum is the total variance.

What we want to do is to decompose this variance into two parts, a within-group part and a between-groups part. I think the second is easier to explain, so let me take that route. To eliminate within group variation, we just substitute the average value in the group for the actual value. This means that we are looking at the following chart instead:

The blue slanted line is the average in each state. We see visually that much of the variation has gone away, so we would expect most variation to be within a state rather than between states.

The idea is that we measure the variation using the first approach and we measure the variation using the second approach. The ratio of these two values tells us how much of the variation is due to between-groups changes. The remaining variation must be due to within-group variation. The next section shows the calculation in SQL.

Doing the Calculation in SQL
Expressing this in SQL is simply a matter of calculating the various sums of squared differences. The following SQL statement calculates both the within-group and between-group variation:

SELECT (SUM((g.grpval - a.allval)*(g.grpval - a.allval))/
........SUM((d.val - a.allval)*(d.val - a.allval))
.......) as between_grp,
.......(SUM((d.val - g.grpval)*(d.val - g.grpval)) /
........SUM((d.val - a.allval)*(d.val - a.allval))
.......) as within_grp
FROM (SELECT state as grp, population as val
......FROM censusfiles.zipcensus zc
.....) d JOIN
.....(SELECT state as grp, AVG(population) as grpval
......FROM censusfiles.zipcensus zc
......GROUP BY 1
.....) g
.....ON d.grp = g.grp CROSS JOIN
.....(SELECT AVG(population) as allval
......FROM censusfiles.zipcensus zc
.....) a

First note that I snuck in the calculation for both within- and between- group variation, even though I only explained the latter.

The from clause has three subqueries. Each of these calculates one level of the summary -- the value for each zip, the value for each state, and the overall value. All the queries rename the fields to some canonical name. This means that we can change the field we are looking at and not have to modify the outer SELECT clause -- a convenience that reduces the chance of error.

In addition, the structure of the query makes it fairly easy to use a calculated field rather than just a column. The same calculation would need to be used for all the fields.

And finally, if you are using a database that supports window functions -- such as SQL Server or Oracle -- then the statement for the query can be much simpler.

Discussion of Results
The results for population say that 12.6% of the variation in zip code population is between states and 87.4% is within states. This confirms the observation that using the state averages removed much of the variation in the data. In fact, for most of the census variables, most of the variation is within states.

There are definitely exceptions to this. One interesting exception is latitutude (which specifies how far north or south something is). The within-state variation for latitude is 5.5% and the between-state is 94.5% -- quite a reversal. The scatter plot for latitude looks quite different from the scatter plot for population:


In this scatter plot, we see that the zip code values in light blue all fall quite close to the average for the state -- and in many cases, quite far from the county average. This makes a lot of sense geographically, and we see that fact both in the scatter plot and in the within-group and between-group variation.

Statistical Approach
Finally, it is instructive to go back to Paul Allison's book and look at his method for doing the same calculation in SAS. Although I am going to show SAS code, understanding the idea does not require knowing SAS -- on the other hand, it might require an advanced degree in statistics.

His proposed method is to run the following statement:

proc glm data=censusfiles.zipcensus;
....absorb state;
....model population=;
run;

And, as he states, "the proportion of variation that is between [states] is just the R-squared from this regression."

This statement is called a procedure (or proc for short) in SAS. It is calling the procedure called "glm", which stands for generalized linear model. Okay, now you can see where the advanced statistics might help.

The "absorb" option creates a separate indicator for each state. However, for performance reasons, "abosrb" does not report their values. (There are other ways to do a similar calculation that do report the individual values, but they take longer to run.)

The "model" part of the statement says what model to build. In this case, the model is predicting population, but not using any input variables. Actually, it is using input variables -- the indicators for each state created on the "absorb" line.

Doing the calculation using this method has several shortcomings. First, the results are put into a text file. They cannot easily be captured into a database table or into Excel. You have to search through lots of text to find the right metric. And, you can only run one variable at a time. In the SQL method, adding more variables is just adding more calculations on the SELECT list. And the SQL method seems easier to generalize, which I might bring up in another posting.

However, the biggest shortcoming is conceptual. Understanding variation between-groups and within-groups is not some fancy statistical procedure that requires in-depth knowledge to use correctly. Rather, it is a fundamental way of understanding data, and easy to calculate using tools, such as databases, that can readily manipulate data. The method in SQL should not only perform better on large data sets (particularly using a parallel database), but it requires much less effort to understand.

Random Samples in SQL

Hi,

How would recommend getting a random sample from a table in SQL? Thank you!

Adam


This is a good question. Unfortunately, there is not a good answer, because the concept of a random sample does not really exist in relational algebra (which SQL -- to a greater or lesser extent -- is based on). There are, however, ways of to arrive at the solution. This discussion is based partly on the Appendix in .

The basic idea is assume that there is a function that returns a random number, say uniformly between 0 and 1. If such a function exists, the SQL code for a random sample might look like:

....SELECT *
....FROM table t
....WHERE rand() <>

The function rand() does actually exist in many databases, such as IBM UDB, Microsoft SQL, and Mysql.

Does this really work for these databases? That depends on whether rand() is a deterministic or non-deterministic function. A deterministic function is essentially evaluated once, when the query is parsed. If this is the case, then all rows would have the same value, and the query would not return a 10% random sample. It would return either 0 rows or all of them.

Fortunately, for these databases, the designers were smart and rand() is non-deterministic, so the above code works as written.

Oracle has a totally different approach. It supports the SAMPLE clause. Using it, the above query would be written as:

....SELECT *
....FROM table t
....SAMPLE (10)

Another approach in Oracle is to use a pseudo-random number generator and ROWNUM. This approach works in any database that has something similar to ROWNUM.

If you happen to be using SAS proc SQL, then you can do something similar to the first example. The only difference is that the function is RAND('UNIFORM') rather than just RAND().