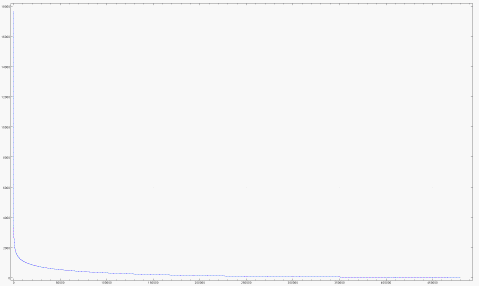
Part of my rater signature is how many movies the rater has rated. A few people (are they really people? Perhaps they are programs or organizations?) have rated nearly all the movies. Most people have rated very few.
A place to read about topics of interest to data miners, ask questions of the data mining experts at Data Miners, Inc., and discuss the books of Gordon Linoff and Michael Berry.

For most data mining algorithms, the best representation of data is a single, flat table with one row for each object of study (a customer or a movie, for example), and columns for every attribute that might prove informative or predictive. We refer to these tables as signatures. Part of the data miner’s art is to create rich signatures from data that, at first sight, appears to have few features.
In our commercial data mining projects, we often deal with tables of transactions. Typically, there is very little data recorded for any one transaction. Fortunately, there are many transactions which, taken together, can be made to reveal much information. As an example, a supermarket loyalty card program generates identified transactions. For every item that passes over the scanner, a record is created with the customer number, store number, the lane number, the cash register open time, and the item code. Any one of these records does not provide much information. On a particular day, a particular customer’s shopping included a particular item. It is only when many such records are combined that they begin to provide a useful view of customer behavior. What is the distribution of shopping trips by time of day? A person who shops mainly in the afternoons has a different lifestyle than one who only shops nights and weekends. How adventurous is the customer? How many distinct SKU’s do they purchase? How responsive is the customer to promotions? How much brand loyalty do they display? What is the customer’s distribution of spending across departments? How frequently does the customer shop? Does the customer visit more than one store in the chain? Is the customer a “from scratch” baker? Does this store seem to be the primary grocery shopping destination for the customer? The answers to all these questions become part of a customer signature that can be used to improve marketing efforts by, for instance, printing appropriate coupons.
The data for the Netflix recommendation system contest is a good example of narrow data that can be widened to provide both a movie signature and a subscriber signature. The original data has very few fields. Every movie has a title and a release date. Other than that, we have very little direct information. We are not told the genre of film, the running time, the director, the country of origin, the cast, or anything else. Of course, it would be possible to look those things up, but the point of this essay is that there is much to be learned from the data we do have, which consists of ratings.
The rating data has four columns: The Movie ID, the Customer ID, the rating (an integer from 1 to 5 with 5 being “loved it.”), and the date the rating was made. Everything explored in this essay is derived from those four columns.
The exploration process involves asking a lot of questions. Often, the answer to one question suggests several more questions.
How many movies are there? 17,770.
How many raters are there? 480,189.
How many ratings are there? 100,480,507.
How are the ratintgs distributed?
 Overall distribution of ratings
Overall distribution of ratings


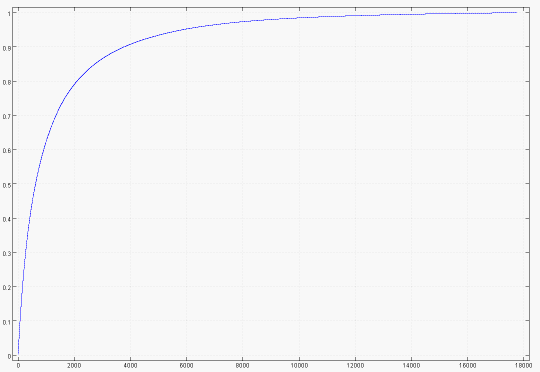
Cumulative proportion of raters accounted for by the most popular movies
Originally posted to a previous version of this blog on 30 April 2007.
As mentioned in a previous post, raters may behave differently when rating new movies than they do when rating old movies. The first step towards investigating that hypothesis is to come up with definitions for "old" and "new."
One possible definition for "new" is that the time between the release date and the rating date is less than some constant. There are several problems with implementing this definition in the Netflix data. One is that, according to the organizers, the release year may sometimes refer to the release of the movie in theaters and in other cases to the release of the movie on DVD. The distribution of release years makes it seem likely that it is usually the date of the release in theaters. Another problem is that although we know when ratings were made to the day, we have only the year of release so the elapsed time from release to rating cannot be measured very accurately.
Another possible definition for "new" is that the time between the rating date and the date the movie was first available for rating on the Netflix site is smaller than some constant. This has the advantage that we can measure it to the day, but suffers from the problem that it does not distinguish between the release of a movie which was recently in theaters from the release to DVD of one that has been in the studio's back catalog for decades.
Whether a movie is new or old, rating behavior may be different when it first becomes available for rating. There may, for instance, be pent-up demand to express opinions about certain movies. A good approximation to when a movie first became available for rating is its earliest rating date. Of course, this only works for movies that became available for rating during the observation period. Any movies that were already available from Netflix before Armistice Day of 1999 will first appear in our data on or shortly after that date. These observations are interval censored. That is, we know only that they became available for rating sometime between 1 January of their release year and 11 November 1999.
The following charts explore the effect of this censoring: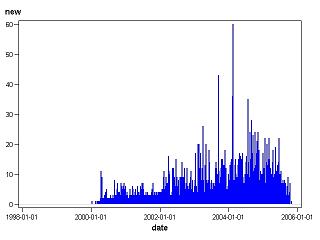 The first chart plots the number of movies having an earliest rating date on each day of the observation period. Only movies with a release year of 2000 or later are included so none of the data is censored. Although the chart is quite spiky, there is nothing special about the first few days, and the overall distribution is similar to the overall distribution of rating counts.
The first chart plots the number of movies having an earliest rating date on each day of the observation period. Only movies with a release year of 2000 or later are included so none of the data is censored. Although the chart is quite spiky, there is nothing special about the first few days, and the overall distribution is similar to the overall distribution of rating counts.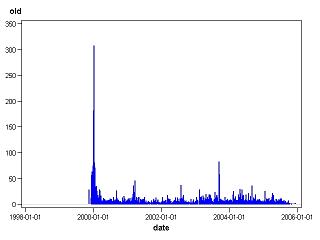
The second chart shows the distribution of earliest observed ratings for movies with release years prior to 2000. There are two interesting things to note. First, the large spike on the left represents movies that were already available for rating prior to the observation period. Second, although all these movies have release dates prior to 2000, the earliest rating dates are distributed across the five-year window similarly to the new releases. This suggests that old movies were becoming available on Netflix at a fairly steady rate across the observation period. At some time in the future, there will be no old movies left to release so all newly available movies will be new. Such shifts in the mixture over time can have a dramatic effect on predictions of future behavior.
Earliest ratings for new and old movies shown together on the same scale: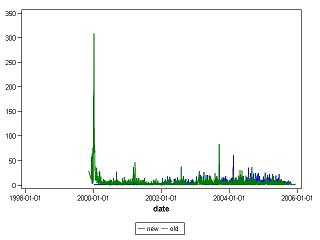
Many people in the Netflix sample rate movies one day and then never rate again. Overall, rating frequency declines over time. In this post, I look at what happens to the probability of making a rating as a function of tenure calculated as days elapsed since the subscriber's first rating. The first chart shows the raw count of ratings by tenure of the subscriber making the rating.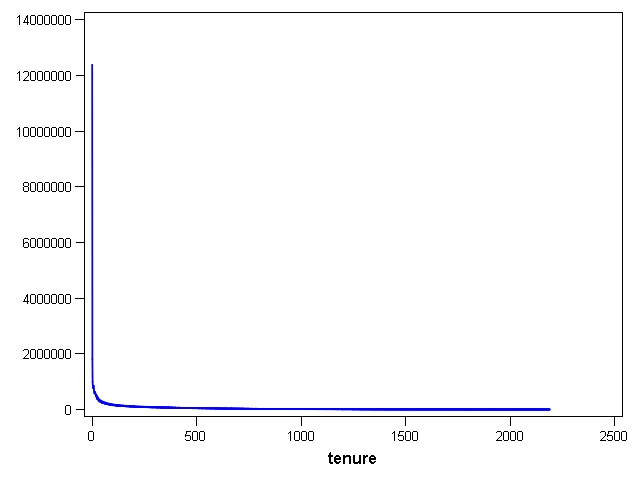
The query that produced this table is: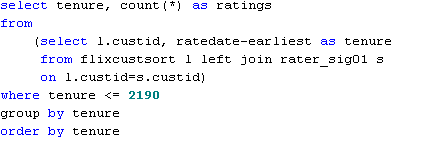
The reason for restricting the results to tenures shorter the 2,190 days is that beyond that ratings are so infrequent that some tenures are not even represented.
While this chart does show clearly that day 0 ratings are by far the most common (by definition, everyone in the training data made ratings on day 0), not much else is visible. In the second chart, the base 10 log of the ratings count is plotted. On this scale, we can see that after an initial percipitous decline, the number of ratings diminishes more slowly of the next 2,000 days and then drops off sharply as we run out of examples of subscribers with very high tenures.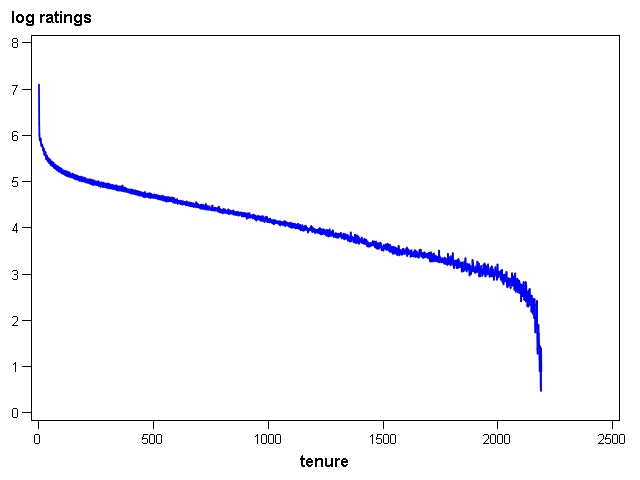
Recall that the earliest rating date in the training data is 11 November 1999 and the latest is 31 December 2005. This means that the theoretical highest observable tenure would be 2,242 days for a subscriber who submitted ratings on the first and last days of the observation period.
The raw count of ratings by tenure is not particularly informative on its own, but it is the first step towards calculating something quite useful: what is the expected number of ratings that a subscriber will make at any given tenure. This can be estimated empirically by dividing the actual count of ratings for each tenure by the number of people who ever experienced that tenure.This is reminiscent of estimating the hazard probability in survival analysis except that one can rate many movies on a single day and making a rating at tenure t is not conditional on not having made a rating at some earlier tenure. You only die once, but you can make ratings as often as you like. For this purpose, I assume that a subscriber comes into existence when he or she first rates a movie and remains eligible to make ratings for ever. In real life, of course, a subscriber could cease to be a Netflix customer, but that does not concern me as that is just one of several reasons that customers are less likely to make ratings over time. For the 2007 KDD Cup challenge, there is no requirement to predict whether customers cancel their subscriptions; only whether they keep rating movies.
The heart of the calculation combines the table created above with another table containing the number of subscribers who ever experienced each tenure.
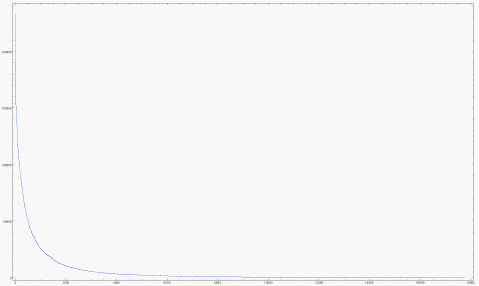
On the first day that people rate movies, they rate a lot of them--over 25 on average. By the next day, their enthusiasm has waned dramatically.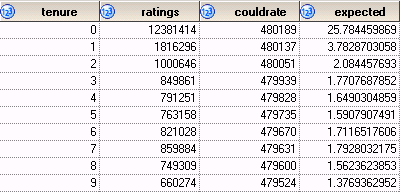
The chart shows the expected number of ratings per day after the first 10 days.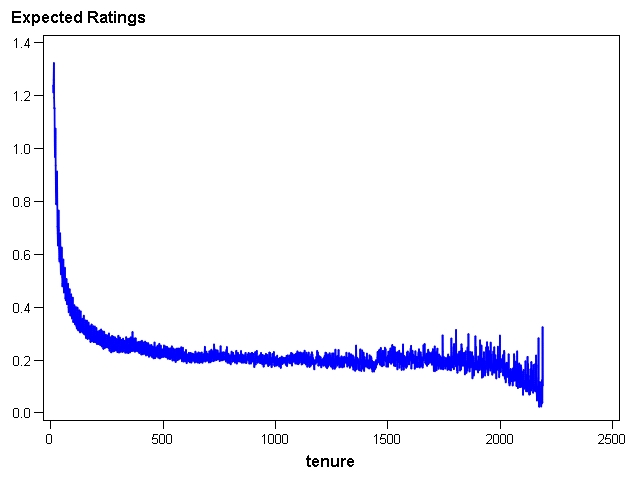
It is not surprising that the variance of the expected number of ratings gets high for higher tenures. The pool of people who have experienced the higher tenures is quite small as seen below.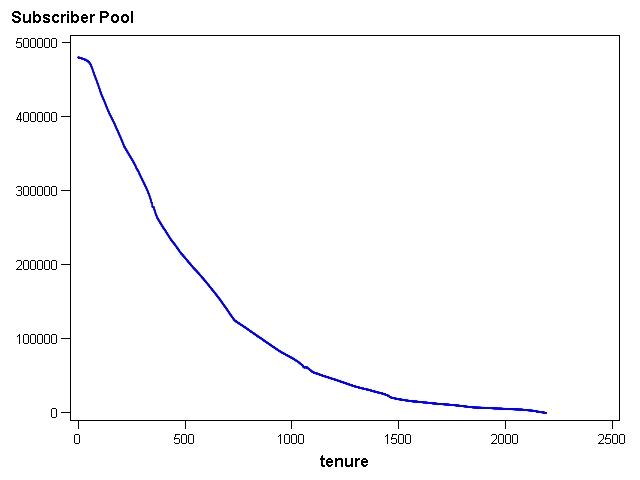
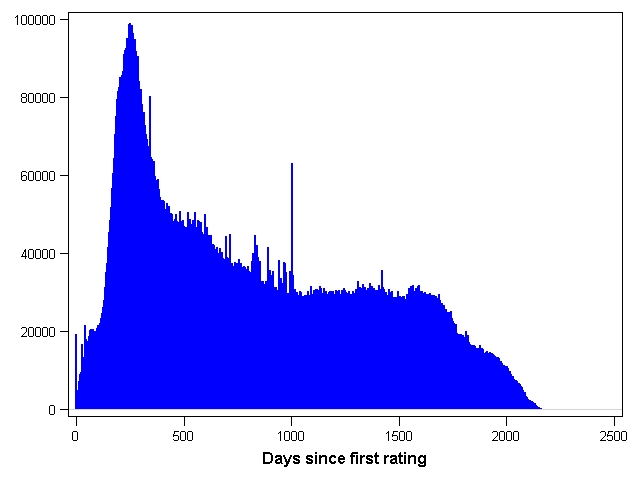 Raw count of ratings by movie age (days since first rating)
Raw count of ratings by movie age (days since first rating)
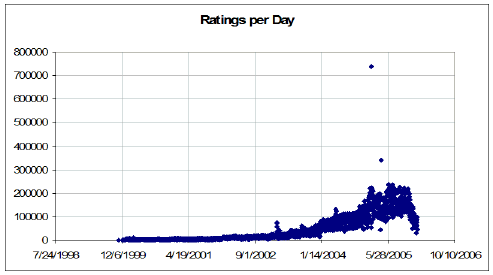 Change in rating activity over the observation period
Change in rating activity over the observation period
In the next chart, I have adjusted the raw number of ratings received for each day since a movie was first rated to take into account the overall level of rating activity on that day. Since the Nth day since first rating comes on a different calendar date for each movie, this adjustment is made at the level of the rating transaction table before summarization. The adjustment is to count each rating as 1 over the total number of ratings that day.
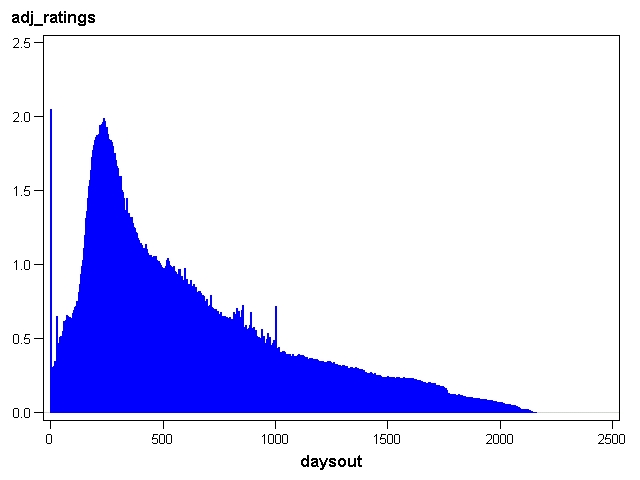 Rating intensity over time adjusted for number of raters
Rating intensity over time adjusted for number of raters
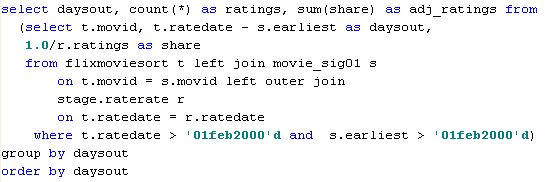
 Comparison of adjusted and unadjusted rating intensity
Comparison of adjusted and unadjusted rating intensity
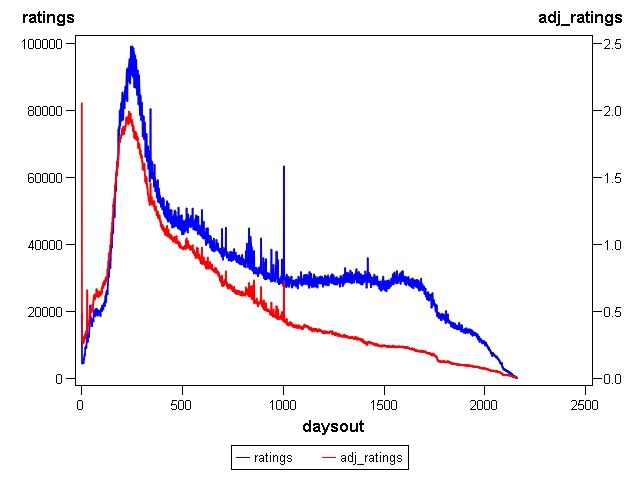
 Movies newly available for rating by date
Movies newly available for rating by date
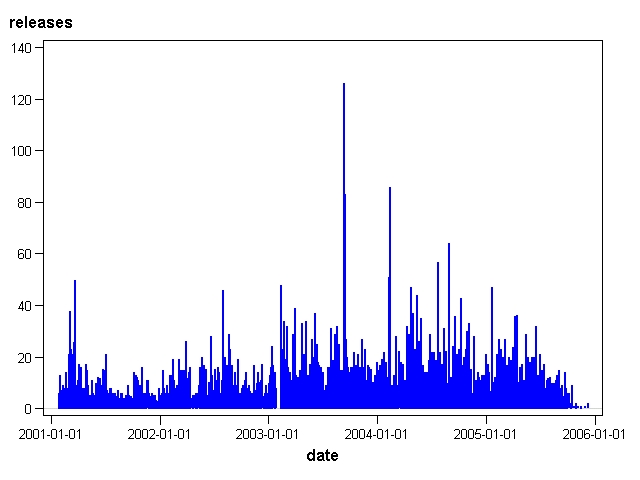
*How many movies of each age were available to be rated?
data atrisk(keep=daysout available);
set releases;
retain available decrease;
daysout = _N_-1;
if daysout = 0 then available=15405;
else available= available-decrease;
decrease=releases;
run;
*Rating activity by days available adjusted for size of pool
proc sql;
create table ratetenure_adj as
select l.daysout, l.ratings,
l.ratings/r.available as rpm,
l.adj_ratings/r.available as arpm
from ratetenure3 l, atrisk r
where l.daysout = r.daysout and r.available > 100
order by l.daysout;
c-+/\releases. Number of movies available for rating by age
Number of movies available for rating by age
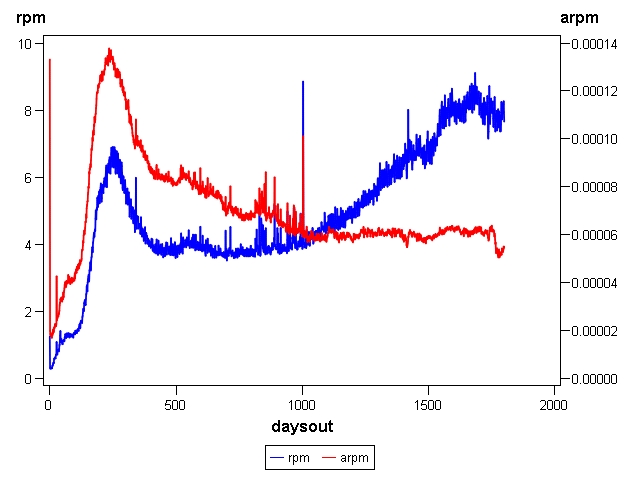 Rating intensity by age of movie
Rating intensity by age of movie