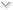Creating Accurate Venn Diagrams in Excel, Part 1

This post (and the next) are about creating accurate Venn diagrams using Excel charts. If you are interested in this, you may be interested in my book Data Analysis Using SQL and Excel.

Recently, I had occasion to analyze prescriber data for a project at a pharmaceutical company. On of the things we wanted to do was to compare visually the prescribing habits of psychiatrists, by places them into three groups: those who only prescribe drug A; those who only prescriber drug B; and those who prescribe both. The resulting chart is:


This chart is an example of a Venn diagram. Unfortunately, Excel does not have a built-in Venn diagram creator. And, if you do a google search, you will get many examples, where the circles are placed manually. Perhaps it is my background in data analysis, but I often prefer accuracy to laziness. So, I developed a method to create simple but accurate Venn diagrams in Excel.

Creating such diagrams is, fundamentally, rather simple. However, there is some math involved. To simplify the math, this post first describes how to create a Venn diagram where the two shapes are squares. In the next post, I'll extend the ideas to using circles.

Creating a Venn diagram requires understanding the following:

1. Creating shapes in Excel.
2. Calculating the correct overlap of the shapes.
3. Putting it all together.
   

This post discusses each of these.

Creating a Shape in Excel

How does one create a shape using Excel charts. The simple answer here is using the scatter plot. If we want to make a square, we can simply plot the four corners of the square and connect them using lines, as in the following example:


Here the square has an area of 81, so each side is exactly nine units long. It is created using five data points:

	X-Value	Y-Value
	-4.50	-4.50
	-4.50	4.50
	4.50	4.50
	4.50	-4.50
	-4.50	-4.50

Notice that the first point is repeated twice. Otherwise, there would be four points, but only three sides.

A small challenge in doing this is making the chart look like a square instead of a rectangle. Unfortunately, Excel does not make it easy to adjust the size of a chart, say by right clicking and just entering the width and height.

One way to make the chart square is to place it in a single cell and then adjust the row height and column height to be equal. My prefered method is just to eye-ball it. The above chart has a width of six columns and a height of 21 rows.

In this case, the square is centered on the origin. There is a reason for this. The temptation is to have the square be positioned at the origin and then pass through the points (0,9), (9,9), and (9,0). However, I find that when Excel draws the square, the axes interfere with the sides of the square, so some are shaded heavier than others. This happens even when I remove the axes.

As an aside here, you can imagine creating many different types of shapes in Excel besides squares. However, Excel only understands these as lines connecting a scatter plot. In particular, this means that you cannot color the interior of the shape.


Calculating the Overlaps

Assume that we have two squares that overlap, one square has an area of 100 (side is 10) and the other 25 (side is 5). What is the overlap between them?

There is not enough information to answer this question. It is clearly between 0 (if the squares do not overlap) and 25 (the size of the smaller square). If the overlap is 10, how big is the overlap? In the following picture, the area of C is 10.

What are the dimensions of C? The height is the height of the smaller square -- 5. So the width must be 2 (=10/5).

Putting It Together

To put this together for a Venn diagram using squares, we simply need to position two squares given the following information:

• The sizes of the two squares.
• The overlap between them.

Consider the original diagram at the top of this posting. The sizes of the two regions are 13,941 and 11,175 respectively. The overlap is 9,783.

The first thing to calculate is the side length for the two squares:

• 118.07 for the first square (=sqrt(13,941)).
• 105.71 for the second (=sqrt(11,175)).
  

Then, we need to calculate the width of the overlapping region (we already know its height and area):

• 92.54 = 9,783 / 105.71

Now we need to calculate the points for the two squares. The way that I do the calculation is to place square at the origin, and then to add X- and Y- offsets to shift it around the plane. So, the general formula for the points are:

• (0 + X-offset, 0 + Y-offset)
• (side + X-offset, 0 + Y-offset)
• (side + X-offset, side + Y-offset)
• (0 + X-offset, side + Y-offset)
• (0 + X-offset, 0 + Y-offset)

Since we know the side lengths of the two squares, I only need to calculate the offset values. The first square is centered at the origin (rather than starting there), so the offset is - side/2 for both X and Y.

The second square is centered vertically, so its Y-offset is also - side/2. The X-offset is the bigger challenge. In order to get the correct overlap, it is:

• (side-first - X-offset-first) - overlap-width

The attached spreadsheet has these calculations. The data table on the spreadsheet looks like:

		Area	Side	X Offset	Y Offset
	Left	13,941	118.07	-59.04	-59.04
	Right	11,175	105.71	-33.51	52.86
	Overlap	9,783	92.54
	big square		little square
	-59.04	-59.04	72.20	52.86
	-59.04	59.04	-33.51	52.86
	59.04	59.04	-33.51	-52.86
	59.04	-59.04	72.20	-52.86
	-59.04	-59.04	72.20	52.86

The points are listed under "big square" and "little square". The first column is the X value for the big square, the second is the Y value; the third is the X value for the little square and the fourth is the Y value.

After creating the chart, you need to beautify it. I remove the axes and axis' labels, thicken the lines around the squares, and adjust the height and width to make the shape look like a square.

The attached .xls file (venn-20081025.xls) contains all the examples in this post.

The next post extends these ideas to creating Venn diagrams with circles, which are the more typical shape for them. It also shows one way to put some color in the shapes to highlight the different regions.

Rolling and Unrolling Correlated Subqueries in SQL

The subject of correlated subqueries arose recently in a data mining class I was teaching. A student inquired about improving the performance of a particular query, which happened to have a correlated subquery. This posting discusses unrolling correlated subqueries to improve performance as well as the rarer need to use correlated subqueries to increase performance.

Correlated subqueries are SQL queries that contain a nested subquery, where the nested query refers to one or more outside tables. The definition sounds complicated, but an example is worth a thousand words.

My book Data Analysis Using SQL and Excel includes a database of customers, orders, and transactions (which can be downloaded). From such data, we might ask a question such as "What products did customer X order on her or his earliest order date?" A typical way to answer this is with a corrrelated subquery.

SELECT ol.ProductID
FROM orders o JOIN
.....orderline ol
.....ON o.OrderID = ol.OrderID AND
.....o.CustomerID = X
WHERE o.OrderDate = (SELECT MIN(OrderDate)
.....................FROM orders o2
.....................WHERE o2.CustomerID = o.CustomerID)

Since this is standard SQL, all reasonable relational databases should support this syntax. One syntax note: the subquery could optionally contain a "GROUP BY o2.CustomerID" clause.

What is the query doing? It is joining two tables together (orders and orderline) and then restricting the results to a single customer. However, the query is about the products in a particular order, so the WHERE clause selects the particular order -- as the one with the smallest OrderDate. Voila. The query answers the question.

The correlated subquery is in the WHERE clause, buried in the subquery in the line o.OrderID = o2.OrderID. This is placing a restriction on the values in the subquery based on the results of an outer query. Do note that if the WHERE clause were instead o.CustomerID = , then the subquery would not be correlated, since there would be no connection to the outer tables.

So far so good. When we think of how the query runs, we think of iterating through every row in the o2 table and looking to match it to the current value in the o table. If there is an index, so much the better because the query engine can use the index to access the o2 table.

This conceptual approach is, in fact, how most (if not all) query engines optimize such a query. For now, I'm leaving open the question of whether this is a good thing, in order to present the idea of unrolling the subquery.

There are other ways to answer the original question ("What products did Customer X order on his or her earliest order date?"). The following query shows an alternative approach:

SELECT ProductID
FROM orders o JOIN
.....orderlines ol
.....ON o.OrderID = ol.OrderID JOIN
.....(SELECT CustomerID, MIN(OrderDate) as minOrderDate
......FROM orders
......GROUP BY CustomerID) omin
.....ON o.OrderDate = omin.minOrderDate AND
........o.CustomerID = omin.CustomerID
WHERE o.CustomerID = X

This version of the query unrolls the subquery, by creating a summary table with the earliest order date for all customers. The link to the other table is made through an explicit join condition between this summary table and the orders table.

Note that in this particular query, the WHERE clause that chooses the customer could be in the subquery, because the columns in the WHERE clause are in the subquery. However, in the general case, the filter could be using columns not available in the subquery -- such as getting all products that start with the letter "A".

There is a big difference in how this query gets executed versus the earlier version. The big difference is that now the orders need to be grouped to find the earliest order date for all orders. The correlated subquery could use an index and only look at the handful of rows for a given customer. So, the correlated subquery seems to be more efficient.

If the correlated subquery is more efficient, then why do I personally avoid using them? One reason is the explicitness of the joins. I find it much easier to understand the unrolled version. However, ease of understanding is less important than performance. In many cases, the unrolled version does execute faster.

Notice that both these queries are looking for data about one particular customer -- a small subset of the overall data. For queries that are looking for such needles in the haystack, then correlated subqueries are fine.

However, decision support queries are usually looking to sift through the whole haystack and not look for just the needle. If we changed the question to "What products are ordered on the earliest order date?" then the queries lose the restrictive clause limiting them to one customer. Now what happens?

In the case of the correlated subquery, query engines essentially execute the joins in one of two ways: (1) by repeatedly looping through one table (typically the one in the inner join) or (2) using indexes. In terms of join algorithms, these are nested loop joins and index-based joins -- two perfectly good join algorithms. But, I might add, two out of many algorithms that could be used.

On the other hand, doing the explicit join as in the second example allows the query engine to execute the different steps it needs to execute, and then to decide on the best strategies. In particular, when the data is partitioned for simultaneous access on multiple processors, most query engines would forget the parallel possibilities and simply execute the correlated subquery on a single processor.

On the other hand, most parallel query engines would correctly parallelize the second version of the query. The GROUP BY would execute in parallel, as would the rest of the joins. The query optimizer would use table statistics to generate the best query plan.

Correlated subqueries are a tool used when designing queries. In all cases, though, the subqueries can be unrolled using more traditional aggregation and join operations. However, query optimizers generally do not perform this operation.

Correlated subqueries are often the most efficient approach when looking for a few rows from a table, particularly when the optimizer can use indexes for the join. On the other hand, unrolling the subqueries is often more efficient when there is a large amount of data, because the optimizer can do full query optimization, making use of parallelism and table statistics.

Currently, most query optimizers do not know how to unrolls correlated subqueries -- or how to roll them back up. So, we need to make such decisions when writing the queries ourselves.

Decision Trees and Clustering

Hi,

I started to write my master thesis and i chose a data mining topic.What I have to do is to analyze the bookings of an airline company and to observe for which markets,time periods and clients the bookings can be trusted and for which not.(The bookings can anytime be canceled or modified ).

I decided to use the decision trees as a classification method but I somehow wonder if clustering would have been more appropriate in this situation.

Thanks and best regards,
Iuliana

When choosing between decision trees and clustering, remember that decision trees are themselves a clustering method. The leaves of a decision tree contain clusters of records that are similar to one another and dissimilar from records in other leaves. The difference between the clusters found with a decision tree and the clusters found using other methods such as K-means, agglomerative algorithms, or self-organizing maps is that decision trees are directed while the other techniques I mentioned are undirected. Decision trees are appropriate when there is a target variable for which all records in a cluster should have a similar value. Records in a cluster will also be similar in other ways since they are all described by the same set of rules, but the target variable drives the process. People often use undirected clustering techniques when a directed technique would be more appropriate. In your case, I think you made the correct choice because you can easily come up with a target variable such as the percentage cancelations, alterations and no-shows in a market.

You can make a model set that has one row per market. One column, the target, will be the percentage of reservations that get changed or cancelled. The other columns will contain everything you know about the market--number of flights, number of connections, ratio of business to leasure travelers, number of carriers, ratio of transit passengers to origin or destination passengers, percentage of same day bookings, same week bookings, same month bookings, and whatever else comes to mind. A decision tree will produce some leaves with trustworthy bookings and some with untrustworthy bookings and the paths from the root to these leaves will be descriptions of the clusters.

A question about decision trees

Hi,

In your experience with decision trees, do you prefer to use a small set of core variables in order to make the model more elegant and/or understandable? At what point do you feel a tree has grown too large and complicated? What are the indicators that typically tell you that you need to do some pruning?

Thank you!

-Adam

Elegance and ease of understanding may or may not be important depending on your model's intended purpose. There are certainly times when it is important to come up with a small set of simple rules. In our book Mastering Data Mining we give an example of a decision tree model used to produce rules that were printed on a poster next to a printing press so the press operators could avoid a particular printing defect. When a decision tree is used for customer segmentation, it is unlikely that your marketing department is equipped to handle more than a handful of segments and the segments should be described in terms of a few famiar variables. In both of these cases, the decision tree is meant to be descriptive.

On the other hand, many (I would guess most) decision trees are not intended as descriptions; they are intended to produce scores of some kind. If the point of the model is to give each prospect a probability of response, then I see no reason to be concerned about having hundreds or even thousands of leaves so long as each one receives sufficient training records that the proportion of responders at the leaf is a statistically confident estimate of the response probability. A very nice feature of decision tree models is that one need not grok the entire tree in order to interpret any particular rule it generates. Even in a very complex tree, the path from the root to a particular leaf of interest gives a fairly simple description of records contained in that leaf.

For trees used to estimate some continuous quantity, an abundance of leaves is very desirable. As estimators, regression trees have the desirable quality of never making truly unreasonable estimates (as a linear regression, for example, might do) because every estimate is an average of a large number of actual observed values. The downside is that it cannot produce any more distinct values than it has leaves. So, the more leaves the better.

The need for pruning usually arises when leaves are allowed to become too small. This leads to splits that are not statistically significant. Apply each split rule to your training set and a validation set drawn from the same population. You should see the same distribution of target classes in both training and validation data. If you do not, your model has overfit the training data. Many software tools have absurdly low default minimum leaf sizes--probably because they were developed on toy datasets such as the ubiquitous irises. I routinely set the minimum leaf size to something like 500 so overfitting is not an issue and pruning is unnecesary.

I have focused on the number of leaves rather than the number of variables since I think that is a better measure of tree complexity. You actually asked about the number of variables. I recommend a two-stage approach. In the first stage, do not worry about how many variables there are or which variable from each family of related variables gets picked by the model. One of the great uses for a decision tree is to pick a small subset of useful variables out of hundreds or thousands of candidates. At a later stage, look at the variables that were picked and think about what concept each of them is getting at. Then pick a set of variables that express those concepts neatly and perhaps even elegantly. You might find, for example, that the customer ID is a good predictor and appears in many rules because customer IDs were assigned serially and long-time customers behave differently than recent customers. Even though this makes perfect sense, it would be hard to explain so you would replace it with a more transparent indication of customer tenure such as "months since first purchase."

Three Questions

Hi Gordon & Michael,

I have a few questions, hope you can help me!

1. While modeling, if we don’t have a very specific client requirement, at what accuracy should we usually stop? Should we stop at 75%, or 80%? Are there standard accuracy requirements based on the industry? For example, in drug research & development, model accuracy is required to be very high.

2. What is the best approach for selecting records/training dataset when the client doesn’t have info on the cut-off/valid ranges for certain numeric columns? If it’s something like Age, there is no problem. But when it’s client/business specific columns, it’s not that easy to figure out the valid ranges. What I usually do for such problems is - 1. do some research on the web to have an understanding on all the values that the specific column can take 2. see the data distribution of that column and select values based on the percentiles. E.g if values from 10 to 60 (for that column) represent 80% of all the records, I exclude all records having values outside this range. Is this a good approach? Are there other alternatives?

3. Generally, I see model accuracy (predictive/risk/churn models) getting better when I recode/transform continuous variables into categorical variables through binning/grouping. But this also results in loss of information. How do we strike a balance here? I believe the business/domain should only decide whether I should use continuous or categorical values, and not the statistics. Is that correct?

Will check your blog regularly for the answersJ

Thanks,

Romakanta Irungbam

These three questions have something in common: There is no single right answer since so much depends on the business context (in the first two cases) or the modeling context (in the third case).

First Question

My statement about no right answers is especially true of the question regarding accuracy. There are contexts where a 95% error rate is perfectly acceptable. I am thinking of response modeling for direct mail. If a model is used to choose people likely to respond to an offer and only 5% of those chosen actually respond, then the error rate is 95%. How could that be acceptable? Well, if a 4% response rate is required for profitability and the response rate for a randomly selected control group is 3% then the model--despite its apparently terrible error rate--has heroically turned a money-losing campaign into a profitable one. Success is measured in dollars (or rupees or yen, but you know what I mean) not by error rates.

In other contexts, much better accuracy is required. A model for credit-card fraud cannot afford a high false-positive rate because this will result in legitimate transactions not being approved. The result is unhappy card holders canceling their accounts. Even if your client cannot provide an explicit requirement for accuracy, you may be able to derive one from the business context.

Absent any other constraints, I tend to stop trying to improve a model when I reach the point of diminishing returns. When a large effort on my part yields only a minor improvement, my time will probably be better spent on some other problem.

Second Question

This question is really about when to throw out data. I see know reason to discard data just because it happens to be in the tails of the distribution. To use your example where 80% of the records have values between 10 and 60, it may be that all the best customers have a value of 75 or more. It may make sense to throw out records which contain clearly impossible values, but even in that case, I would want to understand how the impossible values were generated. If all the records with impossibly high ages were generated in the same geographic region or from the same distribution channel, throwing them out will bias your sample.

Often, unusual values have some fairly simple explanation. When looking at loyalty card data for a supermarket, we found that there were a few cards that had seemingly impossibly large numbers of orders. The explanation was that when people checked out without their card and were therefore in danger of missing out on a discount, the nice checkout lady took pity on them and used her own card to get them the discount. Understanding that mechanism meant we could safely ignore data for those cards since they did not represent the actual shopping habits of any real customer.

Third Question

Whether or not binning continuous variables is helpful or harmful will depend very much on the particular modeling algorithm you are using and on how the binning is performed. I do not agree that, as a general rule, models are improved by binning continuous variables. As you note, this process destroys information. As an extreme example, suppose you have a relationship that is completely determined by a continuous (or discrete, but with small increments) relationship--a tax of a constant amount per liter, say. The more accurately you can measure the number of liters sold, the more accurately you can estimate the tax revenue. In such a case, binning could only be harmful.

When binning tends to be helpful is when the relationship between the explanatory variable and the thing you are trying to explain is more complex than the particular modeling technique you have chosen can handle. For example, you have chosen a linear model and the relationship is non-linear. I once modeled household penetration for my local newspaper, the Boston Globe. One of my explanatory variables was distance from Boston. Clearly, this should have some effect, but there is only a low level of linear correlation. This is because penetration goes up as a function of distance as you travel out to the first ring of suburbs where penetration is highest, but then goes down again as you continue to travel farther from Boston. So a linear model could not make good use of the untransformed variable, but it could make use of three variables in the form within_three, three_to_ten, and beyond_ten (assuming that 3 and 10 are the right bin boundaries). Of course, binning is not the only transformation that could help and linear models are not the only choice of model.

Sorting Cells in Excel Using Formulas, Part 2

In a previous post, I described how to create a new table in Excel from an existing table where the cells in the new table are sorted by some column in the existing table. In addition, the new table is automatically updated when the values in the original table are modified.

The previously described approach, alas, has some shortcomings:

• Only one column can be used for the sort key.
  
• The column must be numeric.
• The column cannot have any duplicate values.
  

This post generalizes on the earlier method by fixing these problems.

If you are interested in this post, you may be interested in my book Data Analysis Using SQL and Excel.


Overview of Simpler Method

The simpler method described in the earlier post recognizes that creating a live sorted table connect to another table consists of the following steps:

1. Ranking the rows in the table by the column to be sorted.
2. Using the rank with the OFFSET() function to create the resulting table.
   

For Step (1), the method uses the built-in RANK() function provided by Excel. This introduces the limitations described above, because RANK() only works on numeric values and produces the same value for duplicates.

The key to fixing these problems is to replace the RANK() function with more general purpose functions.

Instead of RANK()

RANK() determines whether a value is the largest, second largest, third largest, or so on with respect to a list (or smallest, if we are going in the opposite order, which is determined by an optional third argument). One way to think of what it does is that it sorts the values in the list and determines the position of the original value.

An alternative but equivalent way of thinking about the calculation is that it tells us how many values are larger than (or smaller than) the given value. This alternative definition suggests other ways of arriving at the same rankings, such as:

....=COUNTIF(data!B$2:B$55, ">="&data!B2)

This formula can be placed alongside the original table (or anywhere else) and then copied down. It works by counting the number of values that are less than or equal to each value. The resulting ranking is from smallest value to largest value. To reverse the order, simply use "<=" instead. This solves one of the original problems, because the COUNTIF() function works with string data as well as numeric data.

An almost equivalent formulation is to use array functions.

....{=SUM(if(data!B$2:B$55>=data!B2, 1, 0)}

(If you are not familiar with array functions, check out Excel documentation or Data Analysis Using SQL and Excel.)

This is very similar to the COUNTIF() method, although the array functions have one advantage. The conditional logic can be more complicated, so we can do the ranking by multiple columns at the same time.

Using our own version of the rank function fixes two of the three problems. At this point, duplicates still get the same rank value.


Handling Duplicates

The problem with duplicate values is that all these methods assign the same ranking when two different rows have the same value. This makes it impossible to distinguish between the two rows, so one will be included in the sorted table multiple times.

The solution is to fix this problem by adding an offset. If the highest value is repeated multiple times, then all of those rows will have a ranking equal to the number of duplicates. In the following little table, the second column contains the rankings as calculated by either of the above two methods (RANK() does not work because the first column is not numeric):

	a	3
	a	3
	a	3
	b	5
	b	5

What we want, though, is to have distinct values in the second column:

	a	1
	a	2
	a	3
	b	4
	b	5

The solution is to subtract a value from the calculated ranking. This is the number of values that we have already seen that are equal to the value in question. Once again, this can be accomplished with either COUNTIF() or array functions:

....=COUNTIF(data!B$2:B$55, ">="&data!B2) + COUNTIF(data!B$2:B2, "="&data!B2)-1

or

....{=SUM(IF(data!B$2:B$55>=data!B2, 1, 0)) + SUM(IF(data!B$2:B2=data!B2, 1, 0))-1}

These formulations consist of two parts. The first part calculates a ranking, where duplicates get the same value. The second part subtracts the number of duplicates already seen in the list. For the simple example above, the results are actually:

	a	3
	a	2
	a	1
	b	5
	b	4

This works just as well, although it does not preserve the original ordering.

Note that these formulas are all structured so they can be copied down cells and continue working.



What It All Looks Like Together

This method is perhaps best explained by seeing an example. The file sort-in-place.xls contains random information about the fifty states (latitude, longitude, population, and capital for example) on the "data" worksheet. The "data-sorted" worksheet shows the states abbreviations by rank order for each of the columns. For instance, for the size column Alaska is first, followedy by Texas, California, and Montana. For the population columns, the ordering is California, Texas, New York, and Florida. This worksheet using the rankings on the "ranking-countif()" worksheet.

The three worksheets called "ranking-" illustrate the three different methods of doing the rankings -- using RANK(), using COUNTIF(), and using array functions. Note that the RANK() method cannot handle text columns, so it does not work in this case.

If you like, you can change the data on the "data" tab and see the rankings change on the sorted tab. Voila! A sorted table connected by formulas to the original table!

MapReduce Functionality in Commercial Databases

If you use LinkedIn, then you have probably been impressed by their "People you may know" feature. I know that I have. From old friends and colleagues to an occasional person I don't necessarily want to see again, the list often contains quite familiar names.

LinkedIn is basically a large graph of connections among people, enhanced with information such as company names, date of link, and so on. We can imagine how they determine whether someone might be in someones "People you may know category", by using common names, companies, and even common paths (people who know each other).

However, trying to imagine how they might determine this information using SQL is more challenging. SQL provides the ability to store a graph of connections. However, traversing the graph is rather complicated in standard SQL. Furthermore, much of the information that LinkedIn maintains is complicated data -- names of companies, job titles, and dates, for instance.

It is not surprising, then, that they are using MapReduce to develop this information. The surprise, though, is that their data is being stored in a relational database, which provides full transactional-integrity and SQL querying capabilities. The commercial database software that supports both is provided by a company called Greenplum.

Greenplum has distringuished itself from other next-generation database vendors by incorporating MapReduce into its database engine. Basically, Greenplum developed a parallel framework for managing data, ported Postgres into this framework, and now has ported MapReduce as well. This is a strong distinction from other database vendors that provide parallel Postgres solutions, and particularly well suited to complex datatypes encountered on the web.

I do want to point out that the integration of MapReduce is at the programming level. In other words, they have not changed SQL; they have added a programming layer that allows data in the database to be readily accessed using MapReduce primitives.

As I've discussed in other posts, MapReduce and SQL are complementary technologies, each with their own strengths. MapReduce can definitely benefit from SQL functionality, since SQL has proven its ability for data storage and access. On the other hand, MapReduce has functionality that is not present in SQL databases.

Now that a database vendor has fully incorporated MapReduce into its database engine, we need to ask: Should MapReduce remain a programming paradigm or should it be incorporated into the SQL query language? What additional keywords and operators and so on are needed to enhance SQL functionality to include MapReduce?