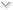Not Enough Data

An article in yesterday's New York Times reminded me of examples of "bad" examples of data mining. By bad examples, I mean that spurious correlations are given credence -- enough credence to make it into a well-reputed national newspaper.

The article, entitled "Eat Quickly, for the Economy's State" is about a leisure time report from the OECD that shows a correlation between the following two variables:

• Change in real GNP in 2008; and,
  
• Amount of time people spend eating and drinking in a given day.

The study is based on surveys from 17 countries (for more information on the survey, you can check this out).

The highlight is a few charts that shows that countries such as Mexico, Canada, and the United States have the lowest time spent eating (under 75 minutes per day) versus countries such as New Zealand, France, and Japan (over 110 minutes per day). The first group of countries have higher growth rates, both in 2008 and for the past few years.

My first problem with the analysis is one of granularity. Leisure time is measured per person, but GNP is measured over everyone. One big component of GNP growth is population growth, and different countries have very different patterns of population growth. The correct measure would be per capital GNP. Taking this into account would dampen the GNP growth figures for growing countries such as Mexico and the United States, and increase the GNP growth figures for lesser growing (or shrinking countries) such as Italy, Germany, and Japan.

Also, the countries where people eat more leisurely have other characteristics in common. In particular, they tend to have older populations and lower (or even negative) rates of population growth. One wonders if speed eating is a characteristic of younger people and leisurely eating is a characteristic of older people.

The biggest problem, though, is that this is, in all likelihood, a spurious correlation. One of the original definitions of data mining, which may still be used in the ecoonomics and political world, is a negative one: data mining is looking for data to support a conclusion. The OECD surveys were done in 17 different countries. The specific result in the NYT article is "Counties in which people eat and drink less than 100 minutes per day grow 0.9% faster -- on average -- than countries in which people each and drink more than 100 minutes per day".

In other words, the 17 countries were divided into two groups, and the growth rates were then measured for each group. Let's look at this in more detail.

How many ways are there to divide 17 countries into 2 groups? The answer is 2^17 = 131,072 different ways (any particular country could be in either group). So, if we had 131,072 yes-or-no survey questions, then would would expect any combination to arise, including the combinations where all the high growth countries are in one group and all the low growth countries in the other. (I admit the exact figure is a bit more than 131,072 but that is unimportant to illustrate my point.)

The situation actually gets worse. The results are not yes-or-no; they are numeric measurements which are then used to split the countries into two groups. The splits could be at any value of the measure. So, any given measurement results in 17-1=16 different possible splits (the first group having the country with the lowest measurement, with the two lowest, and so on). Now we only need about 8,192 uncorrelated measurements to get all possibilities.

However, we do not need all possibilities. A glance at the NYT article shows that the country with the worst 2008 growth is Poland, yet it is in the fast-eating group. And Spain -- in the slow eating group -- is the third fastest growing economy (okay, its GNP actually shrank but less than most others). So, we only need an approximation of a split, where the two groups look different. And then, voila! we get a news article.

The problem is that the OECD was able to measure dozens or hundreds of different things in their survey. My guess is that measures such as "weekly hours of work in main job," "time spent retired," and "time spent sleeping" -- just a few of the many possibilities -- did not result in interesting splits. Eventually, though, a measure such as "time spent eating and drinking" results in a split where the different groups look "statistically significant" but they probably are not. If the measure is interesting enough, then it can become an article in the New York Times.

This is probably a problem with statistical significance. The challenge is that a p-value of 0.01 means that something has only a 1% chance of happening at random. However, if we look at 100 different measures, then there is a really, really good chance that one of them will have a p-value of 0.01 or less. By the way, there is a statistical adjustment called the Bonferroni correction to take this into account (this as well as others are described in the Wikipeida).

Fortunately, neither the OECD nor the New York Times talk about this discovery as an example of data mining. It is just poor data analysis, but poor data analysis that can re-enforce lessons in good data analysis. Lately, I have been noticing more examples of articles such as this, where researchers -- or perhaps just journalists -- extrapolate from very small samples to make unsupported conclusions. These are particularly grating when they appear in respected newspapers, magazines, and journals.

Data mining is not about finding spurious correlations and claiming some great discovery. It is about extracting valuable information from large quantities of data, information that is stable and useful. Smaller amounts of data often contain many correlations. Often, these correlations are going to be spurious. And without further testing, or at least a mechanism to explain the correlation, the results should not be mentioned at all.

When There Is Not Enough Data

I have a dataset where the target (continuous variable) variable that has to be estimated. However, in the given dataset, values for target are preset only for 2% while rest of 98% do not have values. The 98% are empty values. I need to score a dataset and give values for the target for all 2500 records. Can I use the 2% and replicate it several times and use that dataset to build a model? The ASE is too high if I use the 2% data alone. Any suggestions how to handle it, please?

Thanks,

Sneha

Sneha,

The short answer to your question is "Yes, you can replicate the 2% and use it to build a model." BUT DO NOT DO THIS! Just because a tool or technique is possible to implement does not mean that it is a good idea. Replicating observations "confuses" models, often by making the model appear overconfident in its results.

Given the way that ASE (average squared error) is calculated, I don't think that replicating data is going to change the value. We can imagine adding a weight or frequency on each observation instead of replicating them. When the weights are all the same, they cancel out in the ASE formula.

What does change is confidence in the model. So, if you are doing a regression and looking at the regression coefficients, each has a confidence interval. By replicating the data, the resulting model would have smaller confidence intervals. However, these are false, because the replicated data has no more information than the original data.

The problem that you are facing is that the modeling technique you are using is simply not powerful enough to represent the 50 observations that you have. Perhaps a different modeling technique would work better, although you are working with a small amount of data. For instance, perhaps some sort of nearest neighbor approach would work well and be easy to implement.

You do not say why you are using ASE (average squared error) as the preferred measure of model fitness. I can speculate that you are trying to predict a number, perhaps using a regression. One challenge is that the numbers being predicted often fall into a particular range (such as positive numbers for dollar values or ranging between 0 and 1 for a percentage). However, regressions produce numbers that run the gamut of values. In this case, transforming the target variable can sometimes improve results.

In our class on data mining (Data Mining Techniques: Theory and Practice), Michael and I introduce the idea of oversamping rare data using weights in order to get a balanced model set. For instance, if you were predicting whether someone was in the 2% group, you might give each of them a weight of 49 and all the unknowns a weight of 1. The result would be a balanced model set. However, we strongly advise that the maximum weight be 1. So, the weights would be 1/49 for the common cases and 1 for the rare ones. For regressions, this is important because it prevents any coefficients from having too-narrow confidence intervals.

Customer-Centric Forecasting White Paper Available

In our consulting practice, we work with many subscription-based businesses including newspapers, mobile phone companies, and software-as-a-service providers. All of these companies need to forecast future subscriber levels. With production support from SAS, I have recently written a white paper describing our approach to creating such forecasts. Very briefly, the central idea is that the subscriber population is a constantly changing mix of customer segments based on geography, acquisition channel, product mix, subscription type, payment type, demographic characteristics, and the like. Each of these segments has a different survival curve. Overall subscriber numbers come from aggregating planned additions and forecast losses at the segment level. Managers can simulate the effects of alternative acquisition strategies by changing assumptions about the characteristics of future subscribers and watching how the forecast changes. The paper is available on our web site. I will also be presenting a keynote talk on customer-centric forecasting on July 1st at the A2009 conference in Copenhagen.

Rexer Analytics Data Mining Survey

Karl Rexer of Rexer Analytics asked us to alert our readers that their annual survey of data miners is ongoing and will be available for a few more days. Click on the title to be taken to the survey page.

MapReduce, Hadoop, Everything Old Is New Again

One of the pleasures of aging is watching younger generations discover pleasures one remembers discovering long ago--sex, porcini, the Beatles. Occasionally though, it is frustrating to see old ideas rediscovered as new ones. I am especially prone to that sort of frustration when the new idea is one I once championed unsuccessfully. Recently, I've been feeling as though I was always a Beatles fan but until recently all my friends preferred Herman's Hermits. Of course, I'm glad to see them coming around to my point of view, but still . . .

What brings these feelings up is all the excitement around MapReduce. It's nice to see a parallel programming paradigm that separates the description of the mapping from the description of the function to be applied, but at the same time, it seens a bit underwhelming. You see, I literally grew up with the parallel programming language APL. In the late 60's and early 70's my father worked at IBM's Yorktown Heights research center in the group that developped APL and I learned to program in that language at the age of 12. In 1982 I went to Analogic Corporation to work on an array processor implementation of APL. In 1986, while still at Analogic, I read Danny Hillis's book The Connection Machine and realized that he had designed the real APL Machine. I decided I wanted to work at the company that was building Danny's machine. I was hired by Guy Steele, who was then in charge of the software group at Thinking Machines. In the interview, all we talked about was APL. The more I learned about the Connection Machine's SIMD architecture, the more perfect a fit it seemed for APL or an APL-like language in which hypercubes of data may be partitioned into subcubes of any rank so that arbitrary functions can be applied to them. In APL and its descendents such as J, reduction is just one of rich family of ways that the results of applying a function to various data partitions can be glued together to form a result. I described this approach to parallel programming in a paper published in ACM SIGPLAN Notices in 1990, but as far as I know, no one ever read it. (You can, though. It is available here.) My dream of implementing APL on the Connection Machine gradually faded in the face of commercial reality. The early Connection Machine customers, having already been forced to learn Lisp, were not exactly clamouring for another esoteric language; they wanted Fortran. And Fortran is what I ended up working on. As you can tell, I still have regrets. If we'd implemented a true parallel APL back then, no one would have to invent MapReduce today.

Thoughts on Understanding Neural Networks

Lately, I've been thinking quite a bit about neural networks. In particular, I've been wondering whether it is actually possible to understand them. As a note, this posting assumes that the reader has some understanding of neural networks. Of course, we at Data Miners, heartily recommend our book Data Mining Techniques for Marketing, Sales, and Customer Relationship Management for introducing neural networks (as well as a plethora of other data mining algorithms).

Let me start with a picture of a neural network. The following is a simple network that takes three inputs and has two nodes in the hidden layer:

Note that this structure of the network explains what is really happening. The "input layer" (the first layer connected to the inputs) standardizes the inputs. The "output layer" (connect to the output) is doing a regression or logistic regression, depending on whether the target is numeric or binary. The hidden layers are actually doing a mathematical operation as well. This could be the logistic function; more typically, though it is the hyperbolic tangent. All of the lines in the diagram have weights on them. Setting these weights -- plus a few others not shown -- is the process of training the neural network.

The topology of the neural network is specifically how SAS Enterprise Miner implements the network. Other tools have similar capabilities. Here, I am using SAS EM for three reasons. First, because we teach a class using this tool, I have pre-built neural network diagrams. Second, the neural network node allows me to score the hidden units. And third, the graphics provide a data-colored scatter plot, which I use to describe what's happening.

There are several ways to understand this neural network. The most basic way is "it's a black box and we don't need to understand it." In many respects, this is the standard data mining viewpoint. Neural networks often work well. However, if you want a technique that let's you undersand what it is doing, then choose another technique, such as regression or decision trees or nearest neighbor.

A related viewpoint is to write down the equation for what the network is doing. Then point out that this equation *is* the network. The problem is not that the network cannot explain what it is doing. The problem is that we human beings cannot understand what it is saying.

I am going to propose two other ways of looking at the network. One is geometrically. The inputs are projected onto the outputs of the hidden layer. The results of this projection are then combined to form the output. The other method is, for lack of a better term, "clustering". The hidden nodes actually identify patterns in the original data, and one hidden node usually dominates the output within a cluster.

Let me start with the geometric interpretation. For the network above, there are three dimensions of inputs and two hidden nodes. So, three dimensions are projected down to two dimensions.

I do need to emphasize that these projections are not the linear projections. This means that they are not described by simple matrices. These are non-linear projections. In particular, a given dimension could be stretched non-uniformly, which further complicates the situation.

I chose two nodes in the hidden layer on purpose, simply because two dimensions are pretty easy to visualize. Then I went and I tried it on a small neural network, using Enterprise Miner. The next couple of pictures are scatter plots made with EM. It has the nice feature that I can color the points based on data -- a feature sadly lacking from Excel.

The following scatter plot shows the original data points (about 2,700 of them). The positions are determined by the outputs of the hidden layers. The colors show the output of the network itself (blue being close to 0 and red being close to 1). The network is predicting a value of 0 or 1 based on a balanced training set and three inputs.

Hmm, the overall output is pretty much related to the H1 output rather than the H2 output. We see this becasuse the color changes primarily as we move horizontally across the scatter plot and not vertically. This is interesting. It means that H2 is contributing little to the network prediction. Under these particular circumstances, we can explain the output of the neural network by explaining what is happening at H1. And what is happening at H1 is a lot like a logistic regression, where we can determine the weights of different variables going in.

Note that this is an approximation, because H2 does make some contribution. But it is a close approximation, because for almost all input data points, H1 is the dominant node.

This pattern is a consequence of the distribution of the input data. Note that H2 is always negative and close to -1, whereas H1 varies from -1 to 1 (as we would expect, given the transfer function). This is because the inputs are always positive and in a particular range. The inputs do not result in the full range of values for each hidden node. This fact, in turn, provides a clue to what the neural network is doing. Also, this is close to a degenerate case because one hidden unit is almost always ignored. It does illustrate that looking at the outputs of the hidden layers are useful.

This suggests another approach. Imagine the space of H1 and H2 values, and further that any combination of them might exist (do remember that because of the transfer function, the values actually are limited to the range -1 to 1). Within this space, which node dominates the calculation of the output of the network?

To answer this question, I had to come up with some reasonable way to compare the following values:

• Network output: exp(bias + a1*H1 + a2*H2)
• H1 only: exp(bias + a1*H1)
• H2 only: exp(bias + a2*H2)
  

Let me give an example with numbers. For the network above, we have the following when H1 and H2 are both -1:

• Network output: 0.9994
• H1 only output: 0.9926
• H2 only output: 0.9749

To calculate the contribution of H1, I use the ratio of the sums of the squares of the differences, as in the following example for H1:

• H1 contribution: (0.9994 - 0.9926)^2 / ((0.9994 - 0.9926)^2 + (0.9994 - 0.9749)^2)

The following scatter plot shows the regions where H1 dominates the overall prediction of the network using this metric (red is H1 is dominant; blue is H2 is dominant):


There are four regions in this scatter plot, defined essentially by the intersection of two lines. In fact, each hidden node is going to add another line on this chart, generating more regions. Within each region, one node is going to dominate. The boundaries are fuzzy. Sometimes this makes no difference, because the output on either side is the same; sometimes it does make a difference.

Note that this scatter plot assumes that the inputs can generate all combinations of values from the hidden units. However, in practice, this is not true, as shown on the previous scatter plot, which essentially covers only the lowest eights of this one.

With the contribution metric, we can then say that for different regions in the hidden unit space, different hidden units dominate the output. This is essentially saying that in different areas, we only need one hidden unit to determine the outcome of the network. Within each region, then, we can identify the variables used by the hidden units and say that they are determining the outcome of the network.

This idea leads to a way to start to understand standard multilayer perceptron neural networks, at least in the space of the hidden units. We can identify the regions where particular hidden units dominate the output of the network. Within each region, we can identify which variables dominate the output of that hidden unit. Perhaps this explains what is happening in the network, because the input ranges limit the outputs only to one region.

More likely, we have to return to the original inputs to determine which hidden unit dominates for a given combination of inputs. I've only just started thinking about this idea, so perhaps I'll follow up in a later post.

--gordon

Neural Network Training Methods

Scott asks . . .

Dear Ask a Data Miner,

I am using SPSS Clementine 12. The Neural Network node in Clementine allows users to choose from six different training methods for building neural network models:

• Quick. This method uses rules of thumb and characteristics of the data to choose an appropriate shape (topology) for the network.

• Dynamic. This method creates an initial topology but modifies the topology by adding and/or removing hidden units as training progresses.

• Multiple. This method creates several networks of different topologies (the exact number depends on the training data). These networks are then trained in a pseudo-parallel fashion. At the end of training, the model with the lowest RMS error is presented as the final model.

• Prune. This method starts with a large network and removes (prunes) the weakest units in the hidden and input layers as training proceeds. This method is usually slow, but it often yields better results than other methods.

• RBFN. The radial basis function network (RBFN) uses a technique similar to k-means clustering to partition the data based on values of the target field.

• Exhaustive prune. This method is related to the Prune method. It starts with a large network and prunes the weakest units in the hidden and input layers as training proceeds. With Exhaustive Prune, network training parameters are chosen to ensure a very thorough search of the space of possible models to find the best one. This method is usually the slowest, but it often yields the best results. Note that this method can take a long time to train, especially with large datasets.

Which is your preferred training method? How about for a lot of data - (a high number of cases AND a high number of input variables)? How about for a relatively small amount of data?


Scott,

Our general attitude with respect to fancy algorithms is that they provide incremental value. However, focusing on data usually provides more scope for improving results. This is particularly true of neural networks, because stable neural networks should have few inputs.

Before addressing your question, there are a few things that you should keep in mind when using neural networks:

(1) Standardize all the inputs (that is, subtract the average and divide by the standard deviation). This puts all numeric inputs into a particular range.

(2) Avoid categorical inputs! These should be replaced by appropriate numeric descriptors. Neural network tools, such as Clementine, handle categorical inputs using something called n-1 coding, which converts one variable into many flag variables, which, in turn, multiplies the number of weights in the network that need to be optimized.

(3) Avoid variables that are highly collinear. These cause "multidimensional ridges" in the space of neural network weights, which can confuse the training algorithms.

To return to your question in more detail. Try out lots of the different approaches to determine which is best! There is no rule that says that you have to decide on one approach initially and stick with it. To test the approaches use a separate partition of the data to see which works best.

For instance, the Quick method is probably very useful in getting results back in a reasonable amount of time. Examine the topology, though, to see if it makes sense (no hidden units or too many hidden units). Most of the others are all about adding or removing units, which can be valuable. However, always test the methods on a test set that is not used for training. The topology of the network may depend on the training set, so that provides an opportunity for overfitting.

These methods are focusing more on the topology than on the input parameters. If the prune method really does remove inputs, then that would be powerful functionality. For the methods that are comparing results, ensure that the results are compared on a validation set, separate from the test set used to calculate the weights. It can be easy to overfit neural networks, particularly as the number of weights increases.

A comment about the radial basis function approach. Make sure that Clementine is using normalized radial basis functions. Standard neural networks use an s-shaped function that starts low and goes high (or vice versa), meaning that the area under the curve is unbounded. RBFs start low, go high, and then go low again, meaning that the area under the curve is finite. Normalizing the RBFs ensures that the basis functions do not get too small.

My personal favorite approach to neural networks these days is to use principal components as inputs into the network. To work effectively, this requires some background in principal components to choose the right number as inputs into the network.

--gordon